Hybrid Functional Maps for Crease-Aware Non-Isometric Shape Matching

Lennart Bastian1*,
Yizheng Xie1*,
Nassir Navab1,
Zorah Lähner2,3,4
1Technical University of Munich, Germany
2University of Siegen, Germany
3University of Bonn, Germany
4Lamarr Institute, Germany
[CVPR 2024]
*Indicates Equal Contribution
Paper Video Code arXiv
*We have added figures to our paper to enhance clarity. We recommend reading the updated version here. For proper citation, you can use our BibTeX at the end of the page.
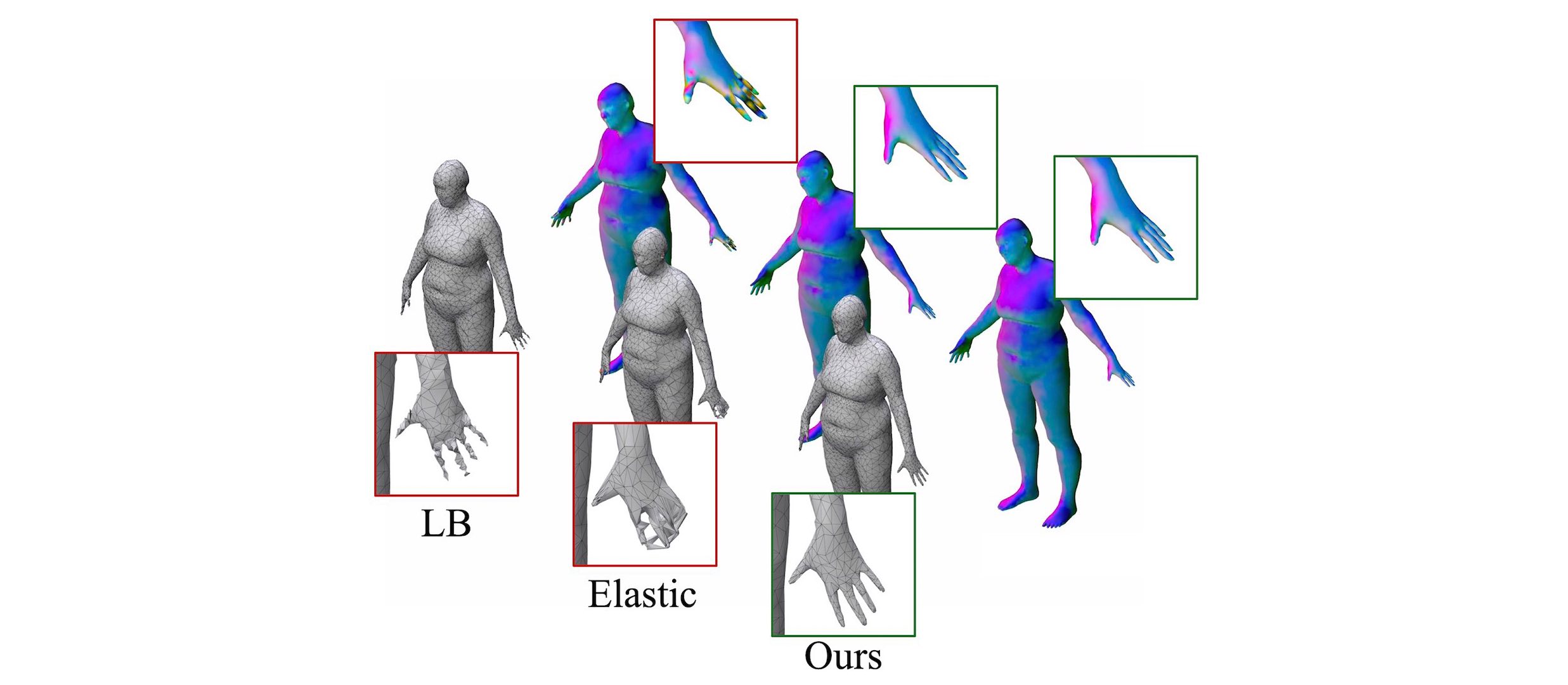
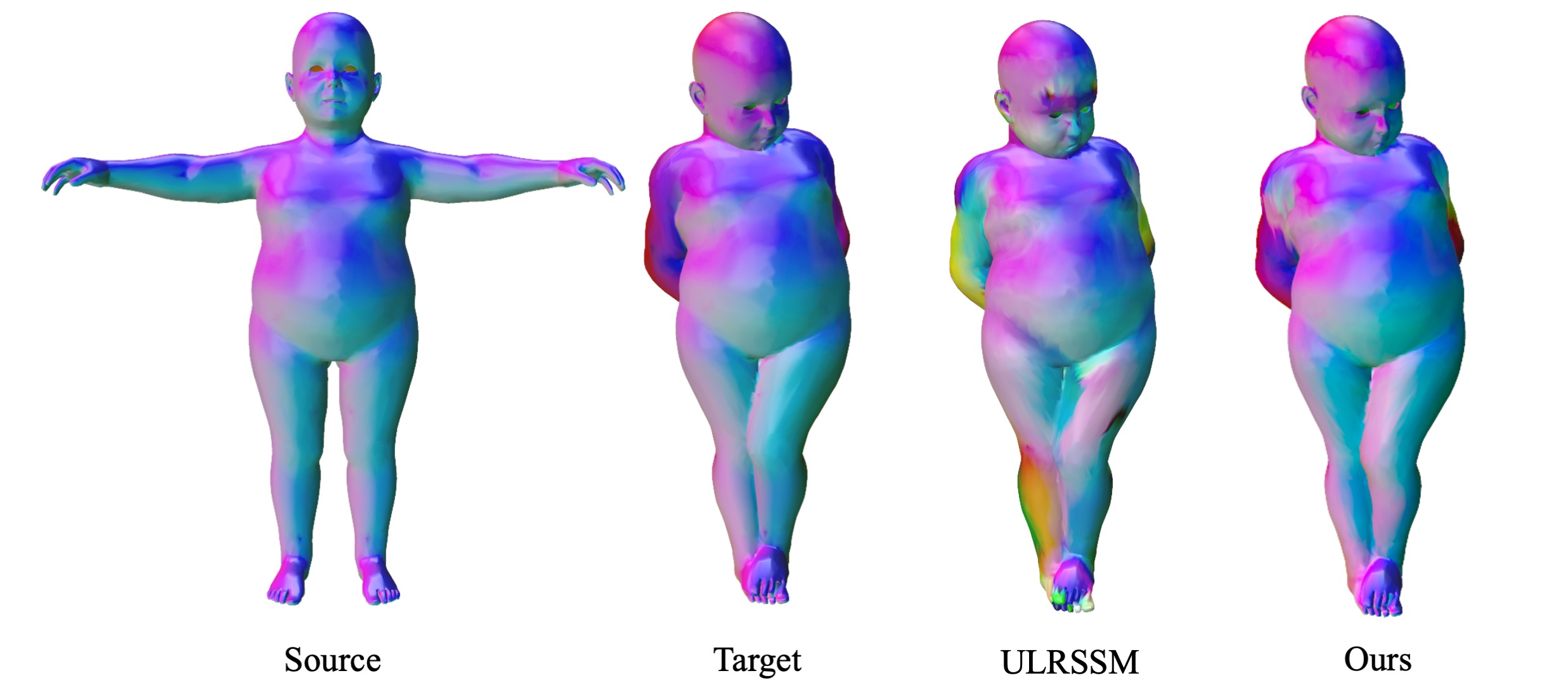
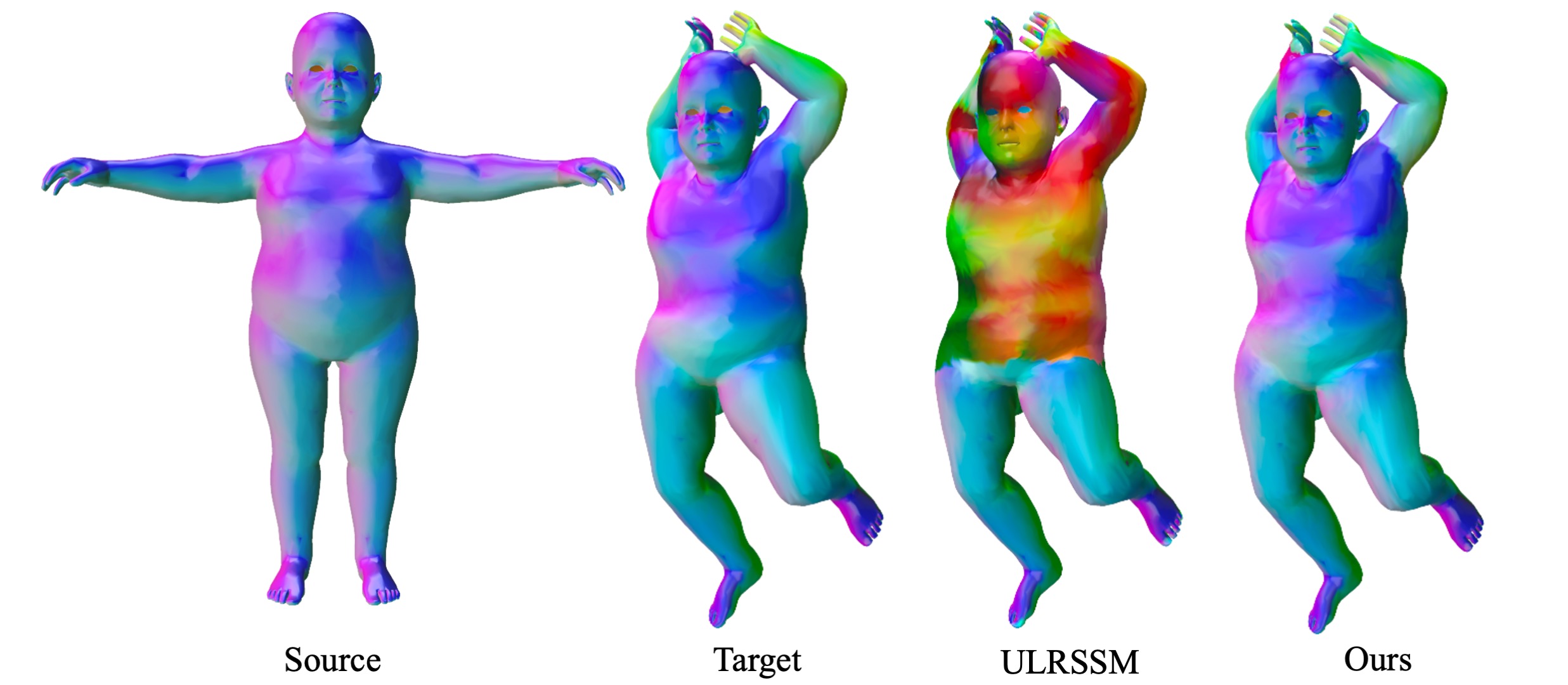
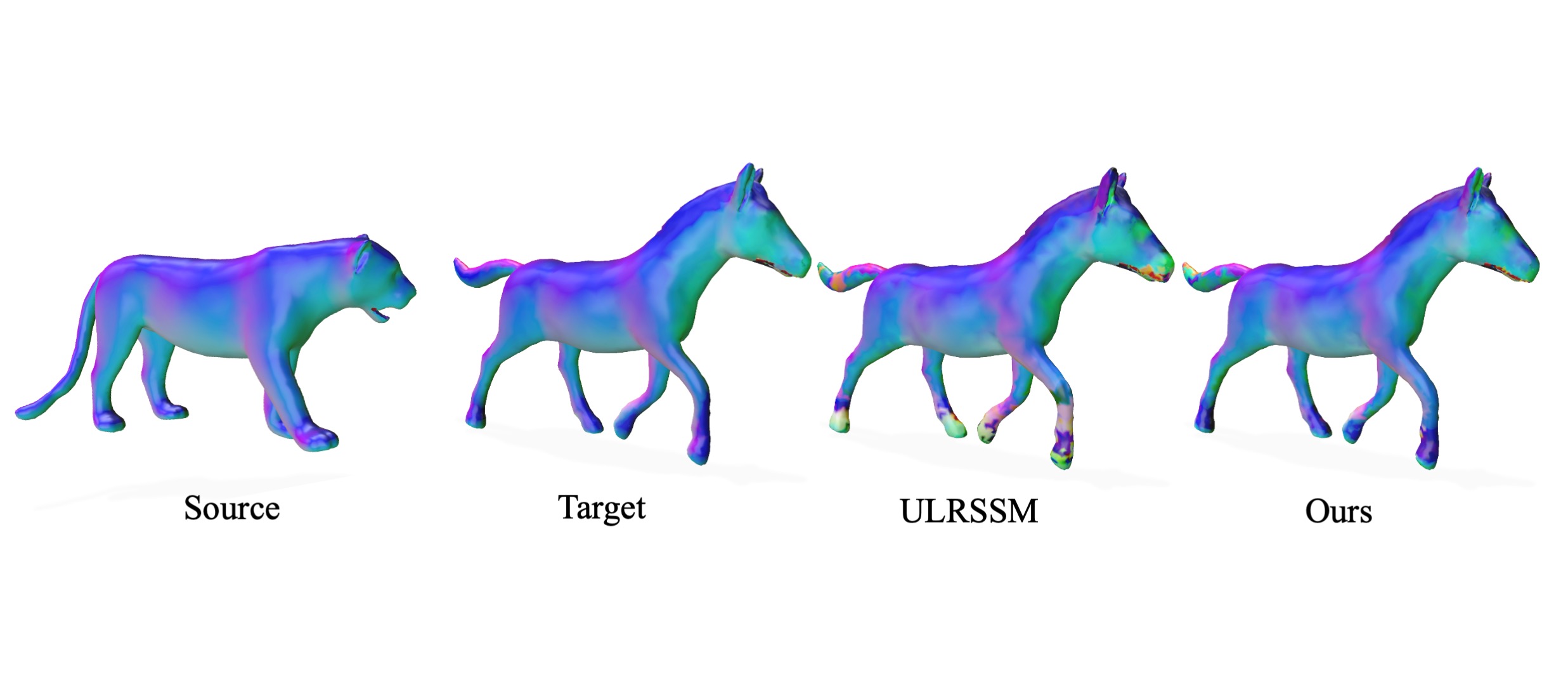
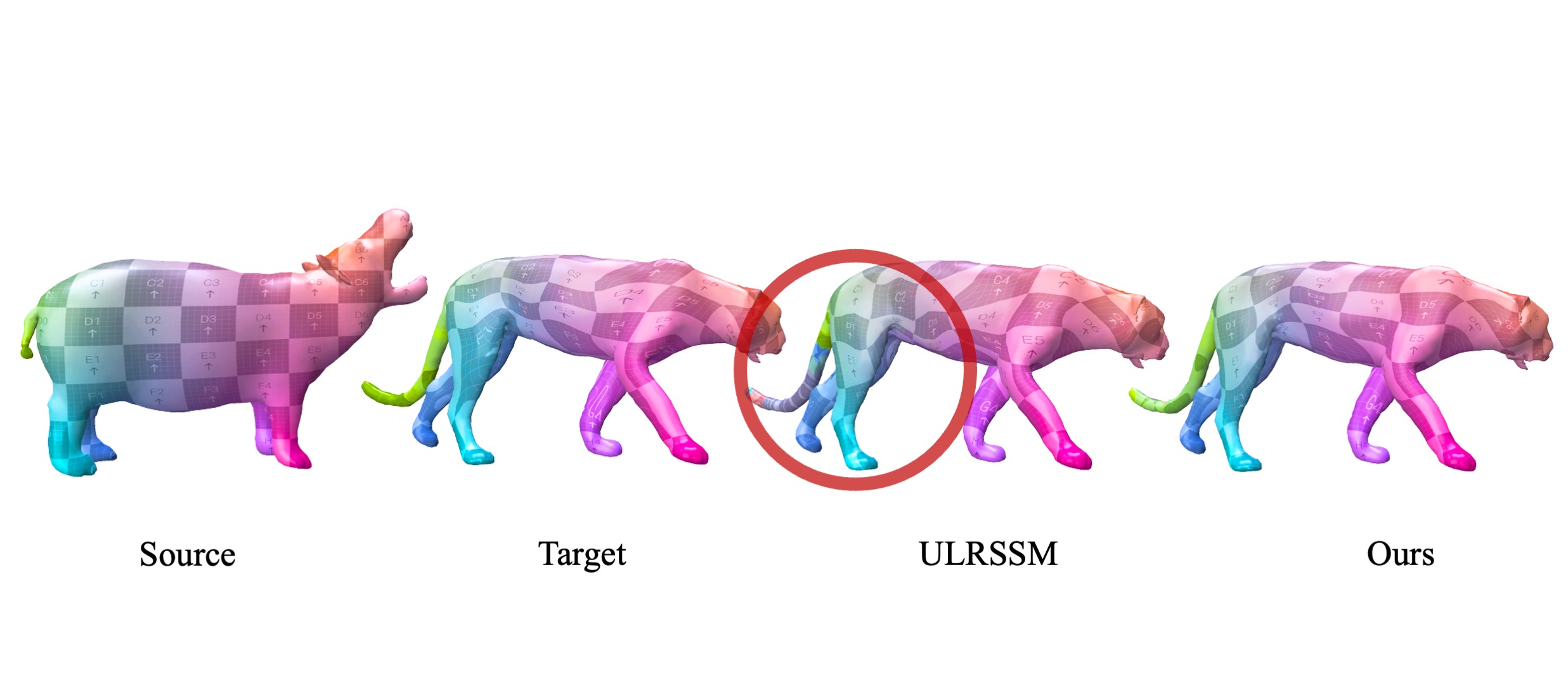
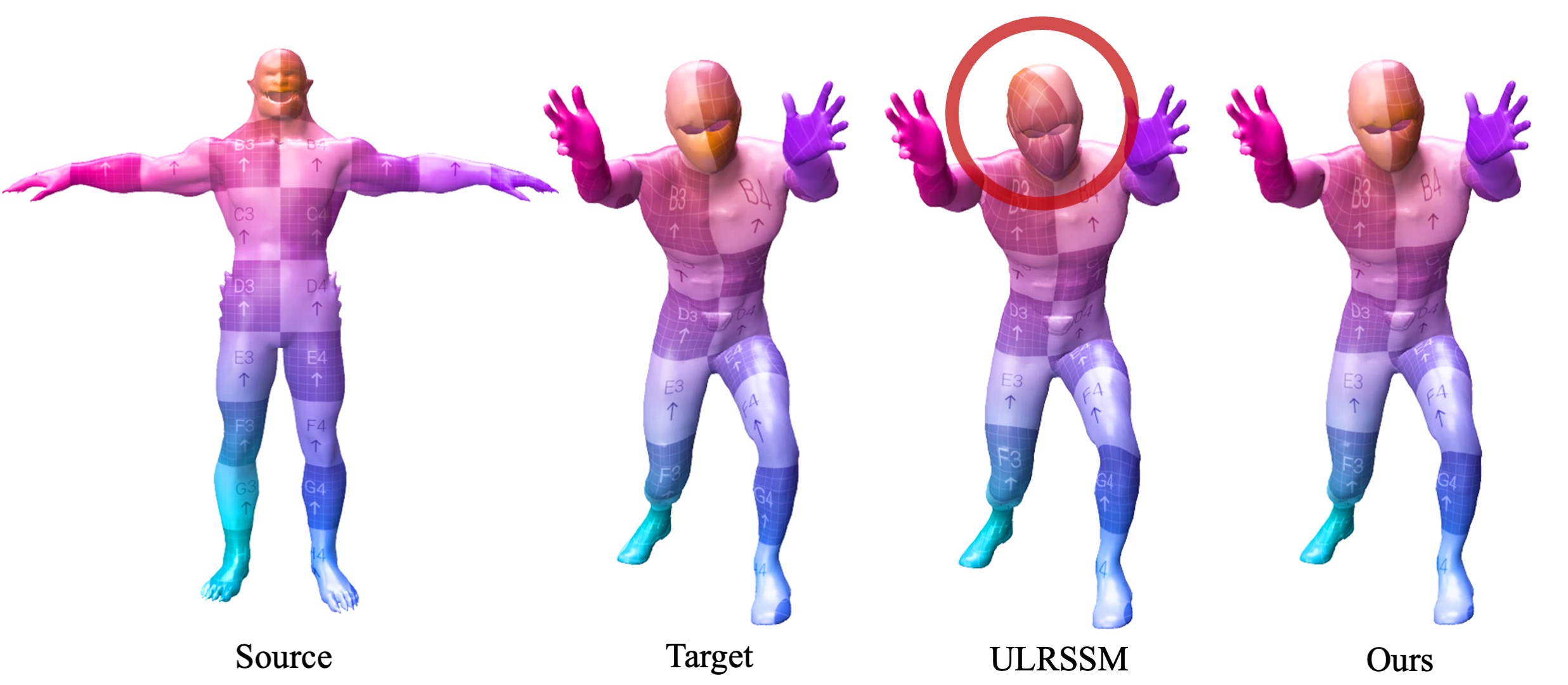
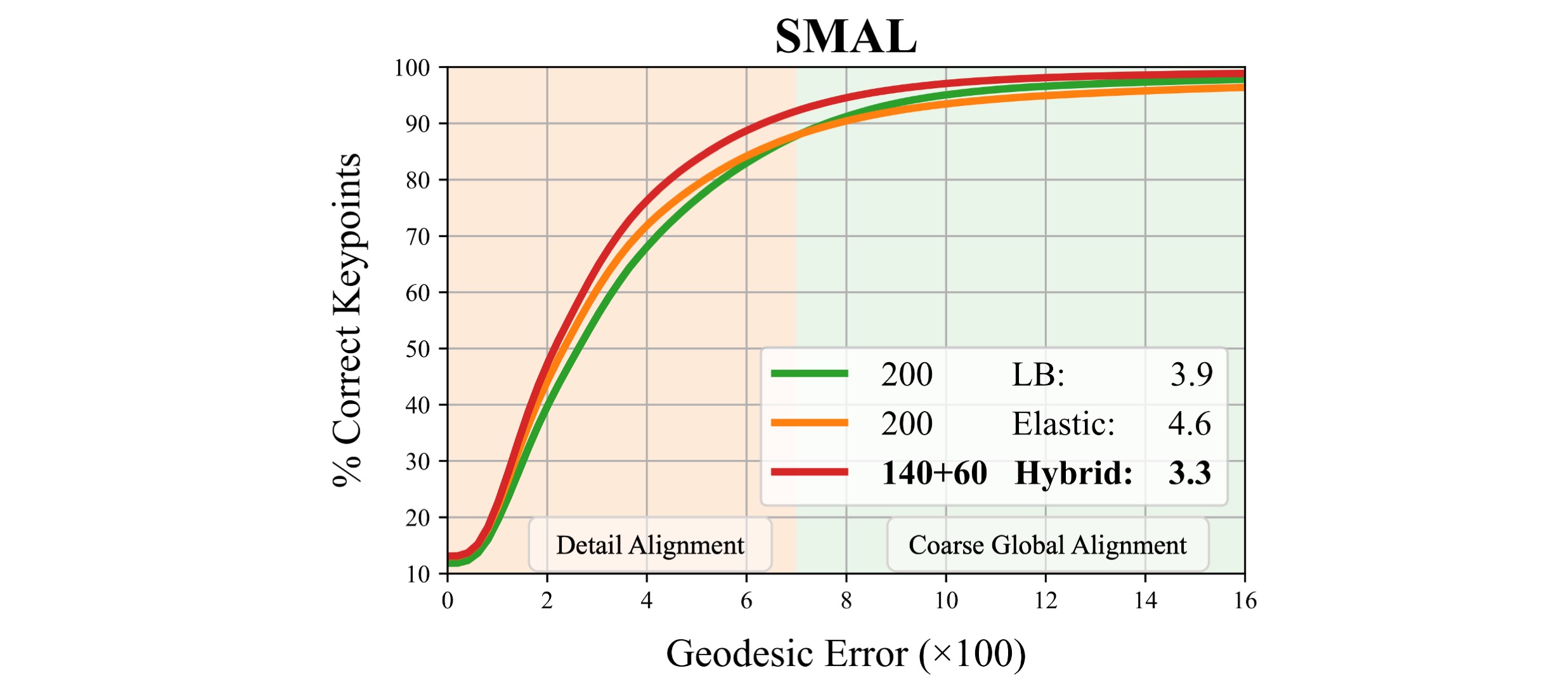
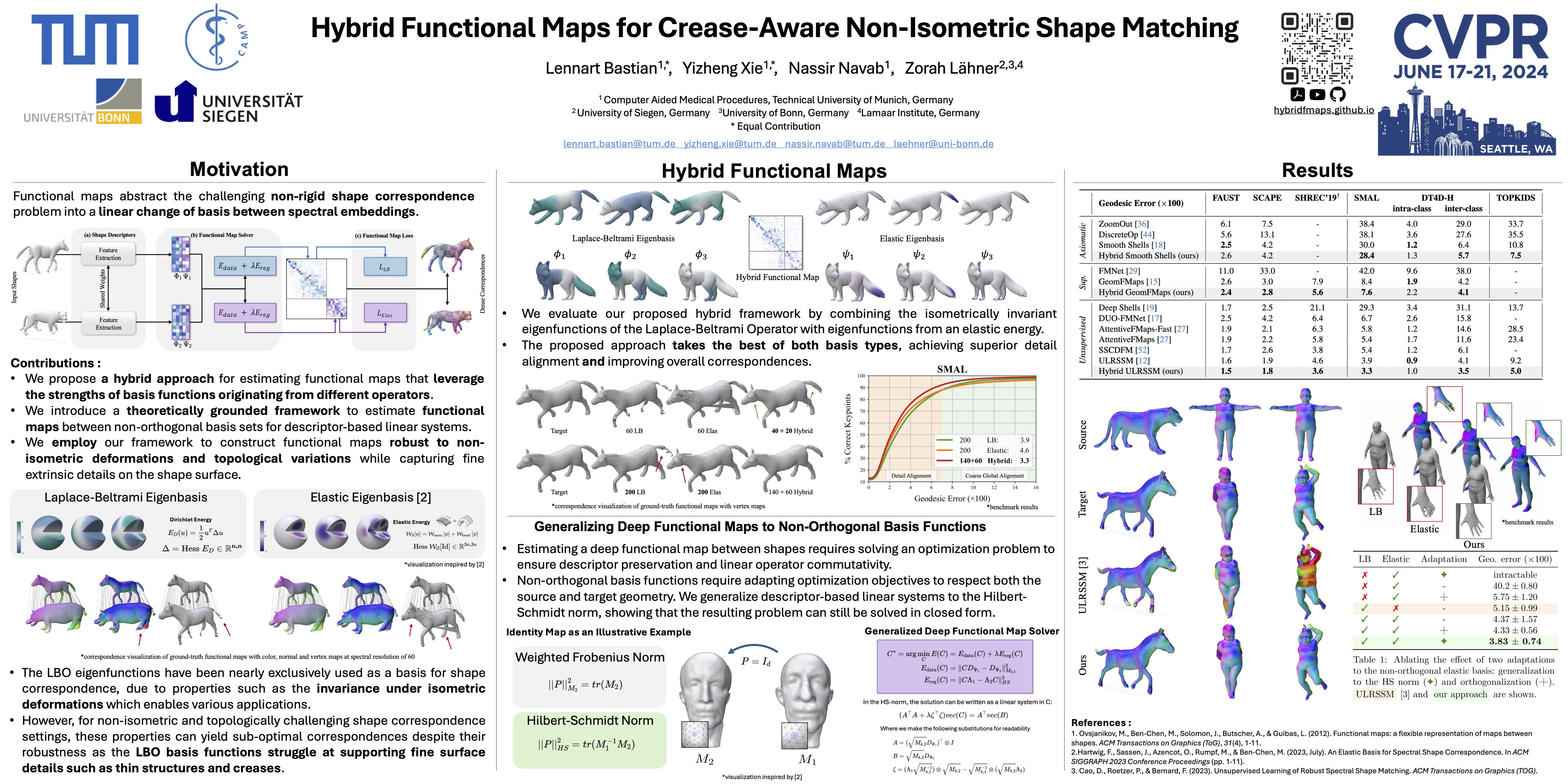
Teaser

We propose a novel approach of hybridizing basis functions originating from different operators, improving performance in near-isometric, non-isometric, and topologically noisy settings.

Abstract

Non-isometric shape correspondence remains a fundamental challenge in computer vision. Traditional methods using Laplace-Beltrami operator (LBO) eigenmodes face limitations in characterizing high-frequency extrinsic shape changes like bending and creases. We propose a novel approach of combining the non-orthogonal extrinsic basis of eigenfunctions of the elastic thin-shell hessian with the intrinsic ones of the LBO, creating a hybrid spectral space in which we construct functional maps. To this end, we present a theoretical framework to effectively integrate nonorthogonal basis functions into descriptor- and learningbased functional map methods. Our approach can be incorporated easily into existing functional map pipelines across varying applications and can handle complex deformations beyond isometries. We show extensive evaluations across various supervised and unsupervised settings and demonstrate significant improvements. Notably, our approach achieves up to 15% better mean geodesic error for non-isometric correspondence settings and up to 45% improvement in scenarios with topological noise.

Left: Laplace-Beltrami operator as hessian of the Dirchlet energy; Right: Hessian of the elastic energy.

hybridfmaps; hybrid maps

First 10 LB eigenbasis, elastic eigenbasis and projected elastic eigenbasis to the normal direction.

Teaser

Correspondence visualization by transferring normal color and vertex positions from source to target shape. Motivationally we show comparison between LB, Elastic and Hybrid basis functions by encoding and recovering a ground truth correspondence through functional map representation.

Teaser

A Percentage-Correct-Keypoint ablation between the pure LB basis, pure elastic basis (orthogonalized), and our hybrid approach at the same spectral resolution (k = 200) from benchmarking results on SMAL with ULRSSM.

Teaser

Teaser

BibTeX

@inproceedings{bastianxie2024hybrid,
        title={Hybrid Functional Maps for Crease-Aware Non-Isometric Shape Matching},
        author={Bastian, Lennart and Xie, Yizheng and Navab, Nassir and L{\"a}hner, Zorah},
        booktitle={Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
        pages={3313--3323},
        month={June},
        year={2024}
      }